
Ein Federpendel besteht in seiner einfachsten Form aus einer Schraubenfeder (mit Federkonstante D) und einem an der Feder aufgehängten Pendelkörper (Massenstück der Masse m). Lenkt man den Pendelkörper gegenüber seiner Gleichgewichtslage nach oben oder unten aus, so beginnt der Pendelkörper auf- und abzuschwingen.
Diese Pendelbewegung soll hier – stark vereinfacht – analysiert werden. Reibungskräfte (innere Reibung der Feder und Luftwiderstand) werden vernachlässigt. Für die Feder wird angenommen, dass das hookesche Gesetz (Proportionalität zwischen Kraft und Dehnung der Feder) exakt gilt. Die Feder wird als masselos betrachtet; daher spielen Kräfte, durch die Teile der Feder beschleunigt werden, in der Rechnung keine Rolle. Torsionsschwingungen, wie sie bei einem realen Federpendel auftreten, sollen nicht berücksichtigt werden.
Zur Beschreibung des momentanen Zustands zur Zeit t wird die Elongation y (Auslenkung gegenüber der Gleichgewichtslage) als Koordinate verwendet. y kann sowohl positiv (nämlich oberhalb der Gleichgewichtslage) als auch negativ sein (unterhalb der Gleichgewichtslage). Als Anfangsbedingung wird angenommen, dass zur Zeit t = 0 der Pendelkörper um die Strecke A angehoben ist und losgelassen wird.

Im linken Teil der Skizze ist die unbelastete Feder abgebildet. In der Mitte ist das komplette Federpendel in seiner Gleichgewichtslage zu sehen; hier ist die Feder durch das Gewicht des Pendelkörpers um eine Strecke y0 gedehnt. Rechts ist ein momentaner Zustand des Federpendels dargestellt, und zwar unter den Voraussetzungen y > 0 und |y| < y0. Die späteren Überlegungen beziehen sich zunächst auf diesen Fall, sind aber auch für andere Werte von y richtig.
Die Dehnung der Feder in der Gleichgewichtslage, hervorgerufen durch die Gewichtskraft FG = m g des Pendelkörpers, ergibt sich aus dem hookeschen Gesetz:

y0 ... Dehnung der Feder in der Gleichgewichtslage
m ... Masse des Pendelkörpers
g ... Fallbeschleunigung (Ortsfaktor)
D ... Federkonstante
Auf den Pendelkörper wirken zwei Kräfte, nämlich die Federkraft und die Gewichtskraft. Die Federkraft berechnet man wieder mit dem hookeschen Gesetz als Produkt der Federkonstante D und der Dehnung y0 − y. Mit Dehnung ist hier die Längenänderung gegenüber der unbelasteten Feder gemeint. Die Federkraft ist in der gezeichneten Situation nach oben gerichtet und erhält deswegen ein positives Vorzeichen. Die Gewichtskraft m g wird dagegen mit einem Minuszeichen versehen, da sie nach unten gerichtet ist.

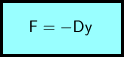
F ... Rückstellkraft
D ... Federkonstante
y ... Elongation
Die letzte Gleichung besagt, dass die auf den Pendelkörper wirkende Kraft (Rückstellkraft) proportional und entgegengesetzt zur Elongation ist. In einem solchen Fall hat man es mit einer ungedämpften harmonischen Schwingung zu tun, die durch eine Sinus- oder Kosinusfunktion beschrieben werden kann. Bemerkenswert ist die Tatsache, dass die Gewichtskraft in der Formel nicht vorkommt.
Eine harmonische Schwingung ist gekennzeichnet durch die so genannte Kreisfrequenz
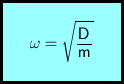
ω ... Kreisfrequenz
D ... Federkonstante
m ... Masse des Pendelkörpers
beziehungsweise die Schwingungsdauer (Periodendauer).

T ... Schwingungsdauer (Periodendauer)
π ... Kreiszahl (3,14159...)
D ... Federkonstante
m ... Masse des Pendelkörpers
Die Elongation y kann nun folgendermaßen als Funktion der Zeit t ausgedrückt werden:

y ... Elongation (Auslenkung gegenüber der Gleichgewichtslage)
A ... Amplitude (maximaler Absolutbetrag der Elongation)
ω ... Kreisfrequenz
t ... Zeit
D ... Federkonstante
m ... Masse des Pendelkörpers
Dass hier eine Kosinus- und keine Sinusfunktion steht, liegt an der oben festgelegten Anfangsbedingung. Setzt man nämlich t = 0 ein, so erhält man – wie gewünscht – die anfängliche Auslenkung y = A. Eine Begründung der Formel soll erst später durch Nachrechnen erfolgen, und zwar im Abschnitt über die Kraft.
v sei die (vorzeichenbehaftete) Geschwindigkeitskomponente in senkrechter Richtung. Bei Bewegung nach oben ist v positiv, bei Bewegung nach unten negativ. v wird berechnet durch Differenzieren (Ableiten) von y nach t, wobei die Kettenregel zu berücksichtigen ist ("Nachdifferenzieren"!).

v ... Geschwindigkeit
A ... Amplitude
ω ... Kreisfrequenz
t ... Zeit
D ... Federkonstante
m ... Masse des Pendelkörpers
Erneutes Einsetzen von t = 0 ergibt v = 0 und bestätigt so, dass die Anfangsbedingung auch hinsichtlich der Geschwindigkeit erfüllt ist: Der Pendelkörper ist beim Loslassen unbewegt.
Differenziert man ein zweites Mal nach t, so erhält man die Beschleunigung a. Auch diese Größe wird hier – entsprechend wie die Geschwindigkeit – mit Vorzeichen verwendet.

a ... Beschleunigung
A ... Amplitude
ω ... Kreisfrequenz
t ... Zeit
D ... Federkonstante
m ... Masse des Pendelkörpers
Die Rückstellkraft auf den Pendelkörper ergibt sich nach dem newtonschen Kraftgesetz (2. Newton-Axiom) als Produkt von Masse und Beschleunigung.

F ... Rückstellkraft
m ... Masse des Pendelkörpers
A ... Amplitude
ω ... Kreisfrequenz
t ... Zeit
D ... Federkonstante
Vergleicht man die Rechenausdrücke für die Kraft F und die Elongation y, so stellt man fest, dass sie sich nur durch ein Minuszeichen und den Faktor D unterscheiden. Es gilt also – in Übereinstimmung mit unserem Ansatz:
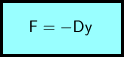
F ... Rückstellkraft
D ... Federkonstante
y ... Elongation
Damit ist die bisher fehlende Begründung der Elongationsformel nachgeholt.
Die kinetische Energie (Bewegungsenergie) des Pendelkörpers ergibt sich durch Einsetzen in die bekannte Formel (halbe Masse mal Quadrat der Geschwindigkeit).
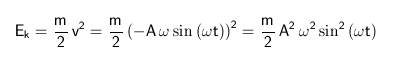

Ek ... kinetische Energie (Bewegungsenergie)
m ... Masse des Pendelkörpers
A ... Amplitude
ω ... Kreisfrequenz
t ... Zeit
D ... Federkonstante
Hinsichtlich der potentiellen Energie (Lageenergie) eines Federpendels herrscht oft Verwirrung. Das liegt daran, dass hier zwei verschiedene Arten potentieller Energie beteiligt sind, nämlich Federenergie und Höhenenergie. Außerdem ist zu beachten, dass die potentielle Energie erst nach Festlegung eines Bezugspunktes, an dem die potentielle Energie den Wert 0 hat, eindeutig bestimmt ist. Hier wird naheliegenderweise vereinbart, dass die beiden genannten Arten potentieller Energie in der Gleichgewichtslage gleich 0 sein sollen.
Für die Federenergie erhält man:

Der Minuend dieser Differenz ergibt sich aus der bekannten Formel für die Federenergie (halbe Federkonstante mal Quadrat der Dehnung). y0 − y ist hier wieder die Dehnung im Vergleich zur unbelasteten Feder. Der Subtrahend ist notwendig, damit für y = 0 der Wert 0 herauskommt.
Der gefundene Rechenausdruck kann folgendermaßen algebraisch umgeformt werden:

Einfacher ist der Rechenausdruck für die Höhenenergie:

Zur Berechnung der gesamten potentiellen Energie braucht man nur noch Ep1 und Ep2 zu addieren, und zwar unter Berücksichtigung der Formel für y0.

Hier fällt auf, dass – ähnlich wie beim Zusammenhang zwischen Rückstellkraft und Elongation – die Höhenenergie nicht mehr vorkommt. Betrachtet man y als Dehnung (im Vergleich zur Federlänge in der Gleichgewichtslage) und nicht wie bisher y0 − y (Dehnung im Vergleich zur Länge der unbelasteten Feder), so kann man die gesamte potentielle Energie als Federenergie auffassen.
Die gesamte potentielle Energie lässt sich entsprechend wie die kinetische Energie ausdrücken:

Ep ... gesamte potentielle Energie (Lageenergie)
D ... Federkonstante
A ... Amplitude
m ... Masse des Pendelkörpers
t ... Zeit
ω ... Kreisfrequenz
Durch Addition von kinetischer und potentieller Energie erhält man die Gesamtenergie. Die Vereinfachung des entsprechenden Terms erfolgt durch Ausklammern der gemeinsamen Faktoren und Anwendung des "trigonometrischen Pythagoras".

Es stellt sich heraus, dass die Gesamtenergie nicht von der Zeit t abhängt. Der Energieerhaltungssatz ist also erfüllt.
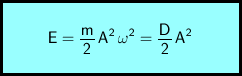
E ... Gesamtenergie
m ... Masse des Pendelkörpers
A ... Amplitude
ω ... Kreisfrequenz
D ... Federkonstante
URL: https://www.walter-fendt.de/html5/phde/springpendulum_math_de.htm
Walter Fendt, 9. September 2007
Letzte Änderung: 13. August 2014